2020大阪大学 物理第1問 力学の雑題
設問I
問1
エネルギー保存則$$\frac{m}{2}v_B^2=mgh$$ $$v_B=\sqrt{2gh}$$
問2
円周上を運動するための条件は、円軌道の中心方向に$$\frac{mv^2}{R}$$の力が働いていることである。この条件でレールからの垂直抗力が決定される。
点Bにおいてレールを離れなければその前後もレールから離れないので(説明すると少々長いから感覚的に当然とする)、点Bにおける垂直抗力\(N\)が正であればよい。
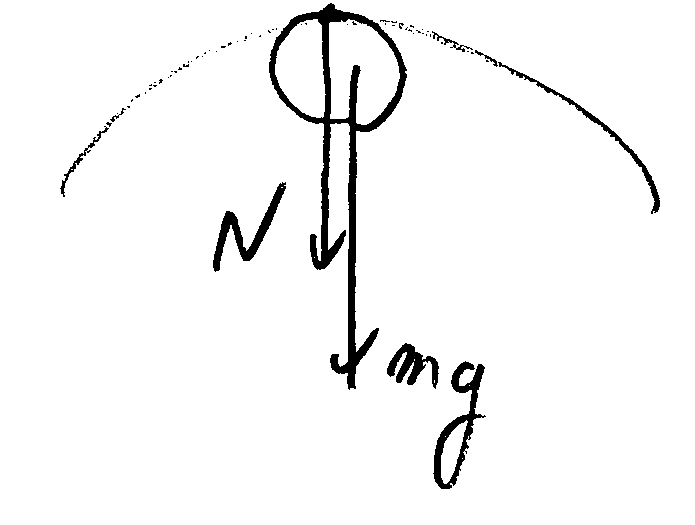
点Bでの中心方向の力から$$mg+N=\frac{mv_B^2}{R}$$よって$$N=\frac{m\cdot 2gh}{R}-mg>0$$解いて$$h>\frac{R}{2}$$
設問II
問3
分裂の前の物体の鉛直方向の速度は0。分裂後の軽い物体の鉛直方向の速度も0。運動量保存より、分裂後の重い物体の速度も0。なので、どちらの物体も鉛直方向の運動は自由落下。
よって、(あ)
問4
水平方向の運動量保存。$$mv_C\cos{\theta}=\frac{3}{4}mv_D$$ $$v_D=\frac{4}{3}v_C\cos{\theta}$$
問5
軽い物体は分裂後から自由落下するので、点Dの真下に落ちる。$$\frac{L}{2}$$
問6
水平方向の速度が\(v_C\cos{\theta}\)のとき落下までに移動する水平距離は\(\frac{L}{2}\)であるので、水平速度が\(\frac{4}{3}v_C\cos{\theta}\)の重い小物体は$$\frac{4}{3}\cdot\frac{L}{2}$$移動する。
よって求める距離は$$\frac{L}{2}\left(1+\frac{4}{3}\right)=\frac{7}{6}L$$
設問III
問7
摩擦がある所での水平方向の運動方程式は、加速度を0として$$\frac{3}{4}ma=-\mu\cdot\frac{3}{4}mg$$ $$a=-\mu g$$
等加速度運動なので、速度が0になる時刻\(t_s\)は$$\frac{4}{3}v_C\cos{\theta}+at_s=0$$ $$ t_S=\frac{4v_C\cos{\theta}}{3\mu g}$$
問8
等加速度運動なので$$x=\frac{4}{3}v_C\cos{\theta}\cdot t+\frac{1}{2}at^2$$ $$3\mu gt^2-8v_C\cos{\theta}t+6x=0$$ $$t=\frac{4v_c\cos{\theta}\pm \sqrt{16v_C^2\cos^2{\theta}-18\mu gx}}{3\mu g}$$ \(t<t_S\)なので$$t=\frac{4v\cos{\theta}-\sqrt{16v_C^2\cos^2{\theta}-18\mu gx}}{3\mu g}$$
問9
エネルギーが失われる要素は「摩擦」と「床と衝突したときの鉛直方向の運動エネルギー」
まず、摩擦によって失われるエネルギーは水平方向の運動エネルギー全てだから$$\frac{1}{2}\cdot\frac{3}{4}m\left(\frac{4}{3}v_C\cos{\theta}\right)^2$$
床と衝突するときの鉛直方向の運動エネルギーは全てD点での位置エネルギーが変換されたものである。D点の高さ\(H\)を求める。
C点からD点までの移動時間を\(T\)とすると、$$v_C\sin{\theta}-gT=0$$解いて$$T=\frac{V_C\sin{\theta}}{g}$$
ゆえに$$\begin{align}H &=v_C\sin{\theta}\cdot\frac{v_C\sin{\theta}}{g}-\frac{g}{2}\left(\frac{v_C\sin{\theta}}{g}\right)^2\\ &=\frac{v_C^2\sin^2{\theta}}{2g} \end{align}$$
また、A点からC点までのエネルギー保存を考えると$$mg(2R+h)=\frac{1}{2}v_C^2$$ $$V_C^2=2g(2R+h)$$
よって、失われたエネルギーは$$\begin{align} &\frac{1}{2}\cdot\frac{3}{4}m\left(\frac{4}{3}v_C\cos{\theta}\right)^2+mgH\\&=\frac{mgv_C^2\sin^2{\theta}}{2g}+\frac{2}{3}mv_C^2\cos^2{\theta}\\ &=\frac{mv_C^2}{6}\left(3+\cos^2{\theta}\right)\\&=\frac{mg}{3}(2R+h)(3+\cos^2{\theta}) \end{align}$$
コメント
よくあるような設定から、定番の問題が並ぶ。落ち着いて対処できるので受験生にはありがたい問題。