私は熱力学第一法則を\(Q=W+\Delta U\) つまり、入る熱量\(Q\)と気体が外にする仕事\(W\) で定義するタイプです。

⑴

状態方程式 \({\rm A}:p_1V_1=RT_1\)なので$${\rm B}: p_1\cdot 3V_1=RT_B$$ $$T_B=3T_1$$ $${\rm C}: \frac{1}{3}p_1\cdot3V_1=RT_C$$ $$T_C=T_1$$

⑵

定圧変化なので$$W_{AB}=p\Delta V=p_1(3V_1-V_1)=2p_1V_1$$ 熱力学第一法則より、$$Q_{AB}=W_{AB}+\Delta U =2p_1V_1+\frac{3}{2}R\Delta T=5RT_1$$

⑶

　定積変化なので\(W_{BC}=0\)。\(Q_{BC}\)が放出する熱量であることに注意して、$$-Q_{BC}=\Delta U$$ $$Q_{BC}=-3RT_1$$

⑷

気体がする仕事は \(\int_C^A pdV\)。すなわち、\(p-V\)グラフにおける曲線(いまは直線)と\(V\)軸で囲まれた部分(いまは台形)の面積の負の値。\(W_{CA}\)はされる仕事であるから、$$W_{CA}=\frac{1}{2}\left(p_1+\frac{1}{3}p_1\right)(3V_1-V_1)$$ $$W_{CA}=\frac{4}{3}RT_1$$

⑸

AからBは定圧変化。状態方程式から\(T=\frac{P}{R}V\) なので直線。

BからCまでは定積変化なので\(V=const\)。直線。

CからAまでは \(p-V\) 図上の直線 \(p=-\frac{p_1}{2V_1}(p-p_1)+V_1\)に沿って変化する。状態方程式と連立して$p$を消去して、$$\begin{align}T&=-\frac{p_1}{3V_1R}V^2+\frac{4p_1}{3R}V\\&=-\frac{p_1}{3RV_1}(V-2V_1)^2+\frac{4}{3}T_1\end{align}$$

よってグラフは下図

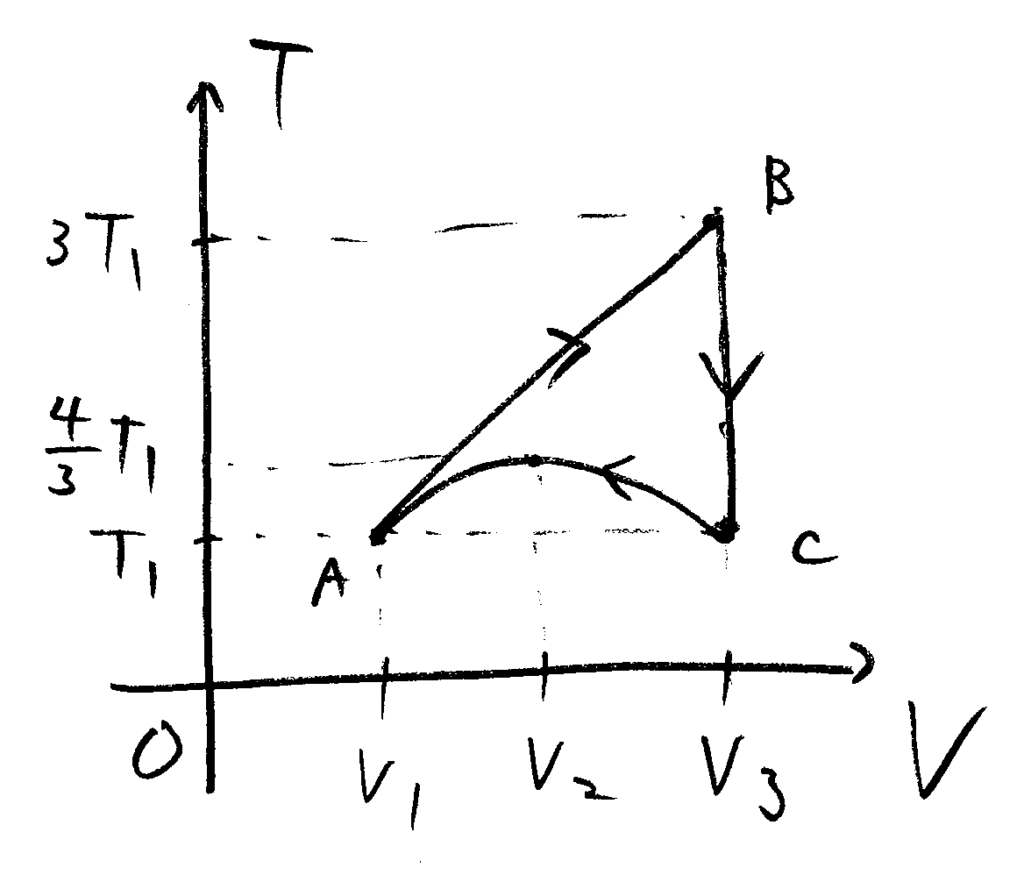
[コメント]サイクルの基本的問題。CからAへの過程は定圧、定積、等温いずれでもないが\(p-V\)図で直線であることから\(p, V\)の関係式が分かるので\(p\)を消去できる。