2020岡山大学 物理第2問 コンデンサのある回路
⑴
十分時間がたつとコンデンサは断線と等価。∴抵抗が直列接続されているだけの回路。
合成抵抗は\(R+3R=4R\)なので流れる電流は\(\frac{V}{4R}\)。∴抵抗1にかかる電圧は$$V_1=\frac{V}{4R}\times R=\frac{1}{4}V$$
⑵
コンデンサの合成容量\(C\)は$$\frac{1}{C}=\frac{1}{C_1}+\frac{1}{C_2}$$なので$$C=\frac{C_1C_2}{C_1+C_2}$$ かかる電圧は\(V\)なので蓄えられた電荷はコンデンサ1, 2ともに$$CV=\frac{C_1C_2V}{C_1+C_2}$$
⑶
PQ間に電流が流れないので、図中のP点とQ点が等電位。抵抗1にかかる電圧は⑴と変わらず\(\frac{1}{4}V\)なので、コンデンサ1にかかる電圧も\(\frac{1}{4}V\)。よってコンデンサ1に蓄えられた電荷\(Q_1\)は$$Q_1=C_1\cdot\frac{1}{4}V=\frac{1}{4}C_1V$$
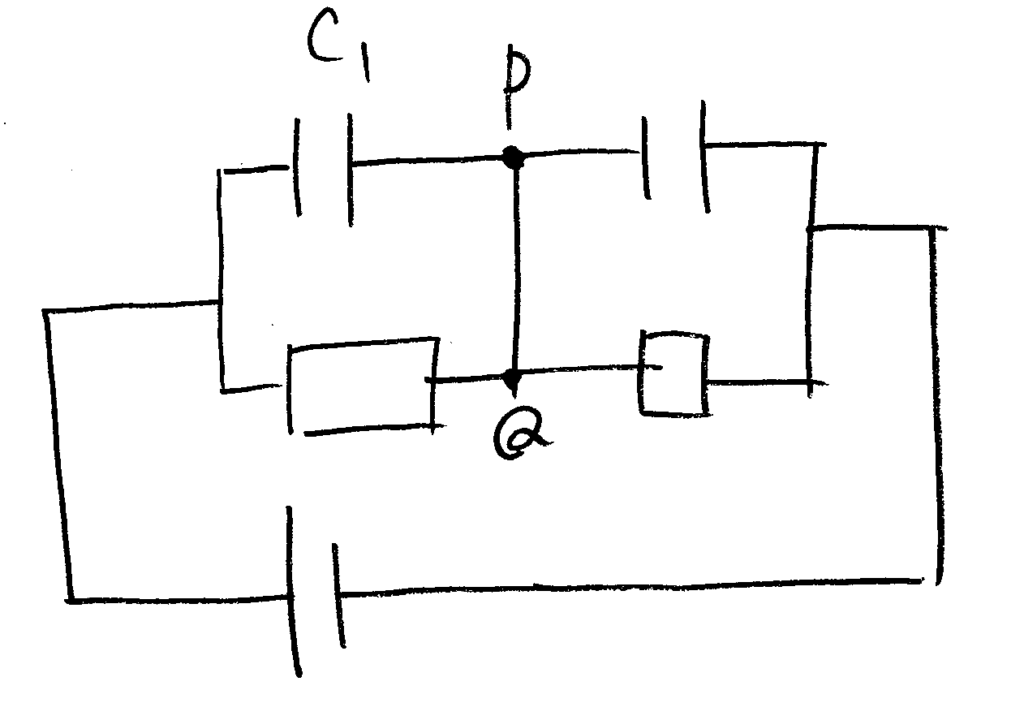
コンデンサ2についても同様に、抵抗2にかかる電圧が\(\frac{3}{4}V\)なので、$$Q_2=\frac{3}{4}C_2V$$
⑷
比誘電率\(\epsilon_\gamma\)のものをコンデンサに詰めると容量が\(\epsilon_\gamma\)倍になる。$$\epsilon_\gamma C_1$$
⑸
合成容量は⑵と同様に計算して、$$C=\frac{\epsilon_\gamma C_1 C_2}{\epsilon_\gamma C_1+C_2}$$
コンデンサ1に蓄えられた電荷\(Q\)は$$Q=\frac{\epsilon_\gamma C_1 C_2}{\epsilon_\gamma C_1+C_2}V$$
スイッチS\(_2\)をいれても電流が流れなかったことから、P点とQ点は等電位。すなわちコンデンサ1にかかる電圧と抵抗1にかかる電圧は等しい。
コンデンサ1にかかる電圧は⑴と同様に\(\frac{1}{4}V\)なので、$$\frac{1}{4}V=\frac{Q}{\epsilon_\gamma C_1} $$ $$\frac{1}{4}=\frac{C_2}{\epsilon_\gamma C_1+C_2}$$
解いて$$\epsilon_\gamma=\frac{3C_2}{C_1}$$
[コメント] これも基本的な問題。「電流が流れない」は「等電位である」と言っているのと同じ。