設問I

問1

直列接続なので、コンデンサの合成容量は$$\frac{C_1C_2}{C_1+C_2}$$ 溜まる電荷\(Q\)は$$Q=\frac{C_1C_2}{C_1+C_2}E$$

よって、コンデンサ2の電圧\(V_1\)は$$V_2=\frac{Q}{C_2}=\frac{C_1}{C_1+C_2}E$$

問2

コンデンサ1は断線されたので、電荷が移動しない。よって、コンデンサ2、コンデンサ3に溜まる電荷をそれぞれ\(Q_2, Q_3\)とすると、$$Q=Q_2+Q_3$$

また、キルヒホッフの法則より$$\frac{Q_2}{C_2}=\frac{Q_3}{C_3}$$これらを連立して解くと$$\begin{align} Q_2&=\frac{C_2}{C_2+C_3}Q\\ &=\frac{C_1C_2^2}{(C_1+C_2)(C_2+C_3)}E \end{align}$$

コンデンサ2の電圧\(V_2\)は$$V_2=\frac{C_1C_2}{(C_1+C_2)(C_2+C_3)}E$$

問3

コンデンサ2とコンデンサ3は並列接続されているので、合成容量\(C_4\)は$$C_4=C_2+C_3$$

この合成コンデンサ4とコンデンサ1の直列接続なので、合成容量は$$\frac{C_1C_4}{C_1+C_4}$$となり$$\begin{align} V_3&=\frac{C_1}{C_1+C_4}E\\&=\frac{C_1}{C_1+C_2+C_3}E \end{align}$$

問4

\(C_3\to \varepsilon_r C_3\)になるので、コンデンサ1の電圧は$$\frac{C_2+\varepsilon_r C_3}{C_1+C_2+\varepsilon_r C_3}E$$

コンデンサ2の電圧は$$\frac{C_1}{C_1+C_2+\varepsilon_r C_3}E$$

コンデンサ2の電圧はコンデンサ1の電圧の2倍なので$$\frac{C_1}{C_1+C_2+\varepsilon_r C_3}E=2\frac{C_2+\varepsilon_r C_3}{C_1+C_2+\varepsilon_r C_3}E$$

解いて$$\varepsilon_r=\frac{C_1-2C_2}{2C_3}$$

設問II

問5

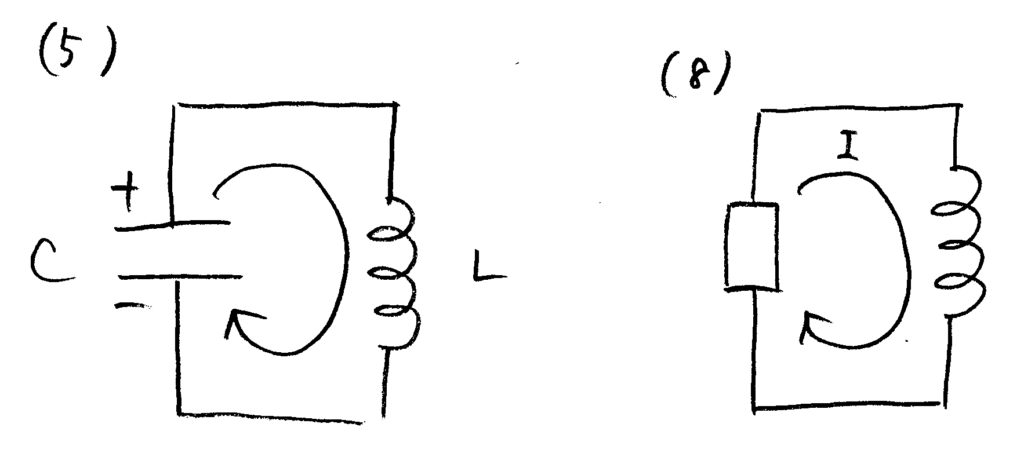
図のように電流の向きと溜まる電荷の正負を定義すると$$\frac{dQ}{dt}=-I$$

キルヒホッフの法則より$$\frac{Q}{C}-L\frac{dI}{dt}=0$$

両辺時間で微分して$$-\frac{I}{C}=L\frac{d^2I}{dt^2}$$

スイッチ4を閉じた時刻を\(t=0\)とすると、初期条件から$$I=I_0\sin{\omega t}, \quad \omega=\frac{1}{\sqrt{LC}}$$

また、$$V=\frac{Q}{C}=L\frac{dI}{dt}$$なので$$V=L\omega I_0\cos{\omega t}$$ \(t=0\)のとき$$E=L\cdot\frac{1}{\sqrt{LC}}I_0$$

解いて$$I_0=E\sqrt{\frac{C}{L}}$$

問6

公式をそのまま使う。\(H_0=nI_0\)

問7

問5より、\(\omega t=\frac{\pi}{2}\)なので$$t=\frac{\pi}{2}\sqrt{LC}$$

問8

キルヒホッフの法則より、$$-I_0R-L\frac{\Delta I}{\Delta t}=0$$ $$\frac{\Delta I}{I_0\Delta t}=-\frac{R}{L}$$

問9

\(t_0\)までは\(\sin\)の関数。(あ)が適する。

問8より$$\frac{dI}{dt}=-\frac{R}{L}I$$なので、$$I=I_0e^{-\frac{R}{L}}t$$であり、(か)が適する。

コメント

これも典型的でやりやすい。不自然さはあるが(問6)、設問で問うことを幅広く取ろうという考えが見て取れる。勉強の成果が出しやすい問題だろう。

他の大学の問題を見ても思うが、微小時間の変化を問う問題が多いので、「微分方程式を扱っている」という認識をもって練習しておくと有利。