回路に対してキルヒホッフの第2法則をバシバシ使っていく。向きに気をつけながら式を立てていけば、それなりにスムーズに進行できる。

問題文では\(\frac{\Delta I}{\Delta t}\)などと書かれていますが、この解答では\(\frac{dI}{dt}\)として微分で考えることもします。

設問⑴

イ）

キルヒホッフを使う。$$-L\frac{\Delta I}{\Delta t}-V=0$$ $$L\frac{\Delta I}{\Delta t}=-V$$

ロ）

\(\Delta Q=C\Delta V\)に\(\Delta Q=I\Delta t\)を代入して$$I\Delta t=C\Delta V$$ $$C\frac{\Delta V}{\Delta t}=I$$

ハ）ニ）

ロ)の式を両辺時間で微分して$$C\frac{d^2V}{dt^2}=\frac{dI}{dt}$$ イ)の式の\(\frac{d I}{dt}\)に代入して$$LC\frac{d^2 V}{dt^2}=-V$$

(単振動の微分方程式と同じなので)解はスイッチを閉じてからの時間を\(t\)として、\(V(0)=\frac{Q_0}{C}\)なので$$V=\frac{Q_0}{C}\cos{\omega t}, \,\, \omega=\frac{1}{\sqrt{LC}}$$

両辺時間で微分して$$\frac{dV}{dt}=-\frac{Q_0\omega}{C}\sin{\omega t}$$

ロ)の式より$$\begin{align} I &=-C \cdot \frac{Q_0\omega}{C}\sin{\omega t} \\&=Q_0\omega\cos{\left(\omega t+\frac{\pi}{2}\right)} \end{align}$$

\(V\)は\(I\)に対して\(\frac{\pi}{2}\)位相が遅れている。

また\(I\)の最大値は$$Q_0\omega=\frac{Q_0}{\sqrt{LC}}$$

設問⑵

ホ）

問題文に書いてあるように、コイルでの電圧降下が0で、ダイオードの方には電流が流れないので、抵抗があるほうだけ電流が流れる。$$E-Ir=0$$ $$I=\frac{E}{r}$$

ヘ）

キルヒホッフを使う。$$E-L\frac{\Delta I}{\Delta t}-V=0$$ $$L\frac{\Delta I}{\Delta t}=-V^\prime$$

ト）

\(V^\prime=V-E\)で、\(E\)は定数なので$$\begin{align} \Delta V^\prime &=\Delta V\\ &=\frac{\Delta Q}{C}\\&=\frac{I\Delta t}{C}\end{align}$$ $$C\frac{\Delta V^\prime}{\Delta t}=I$$

チ）

ハ)のときと同様に、\(I\)も三角関数となる。$$I=I_0\cos{\omega t}$$ \(I=0\)となるとき\(\omega t=\frac{\pi}{2}\)なので$$t=\frac{\pi}{2\omega}=\frac{\pi}{2}\sqrt{LC}$$

問1

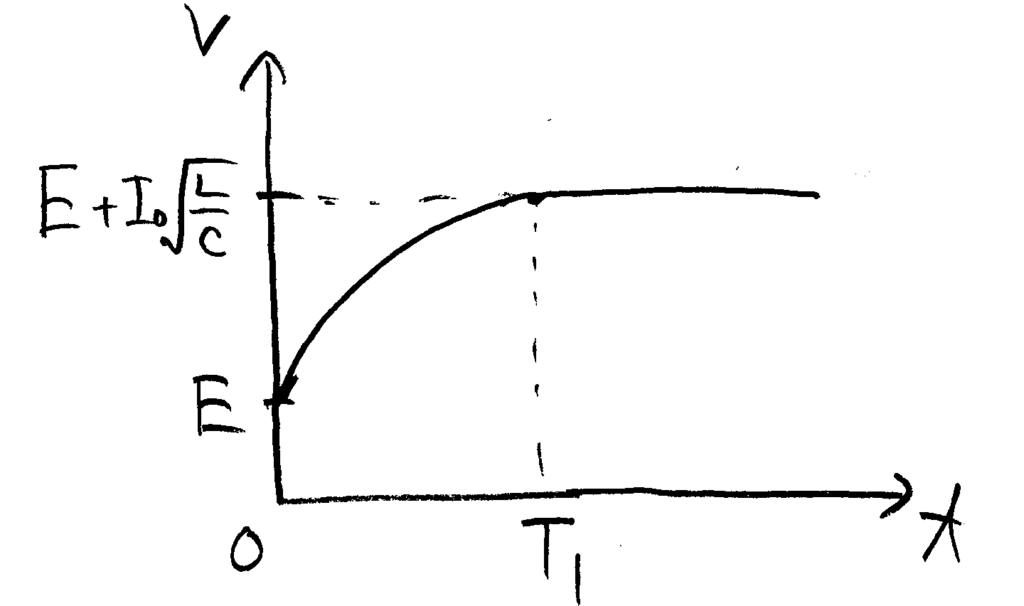
コイル、コンデンサのエネルギーの差分は電源がした仕事に等しい。移動した電荷はコンデンサの電位の変化から\(CV^\prime\)。よって$$\left(0+\frac{1}{2}CV^2\right)-\left(\frac{1}{2}LI_0^2+\frac{1}{2}CE^2\right)=E\cdot C(V-E)$$ $$CV^2-2CEV-LI_0^2+CE^2=0$$ $$V=\frac{EC\pm\sqrt{C^2E^2+CLI_0^2-C^2E^2}}{C}$$ \(V>0\)なので$$V=E+I_0\sqrt{\frac{L}{C}}$$

式ト)より\(V^\prime\)は三角関数なので、グラフは下図。

設問⑶

リ）ヌ）

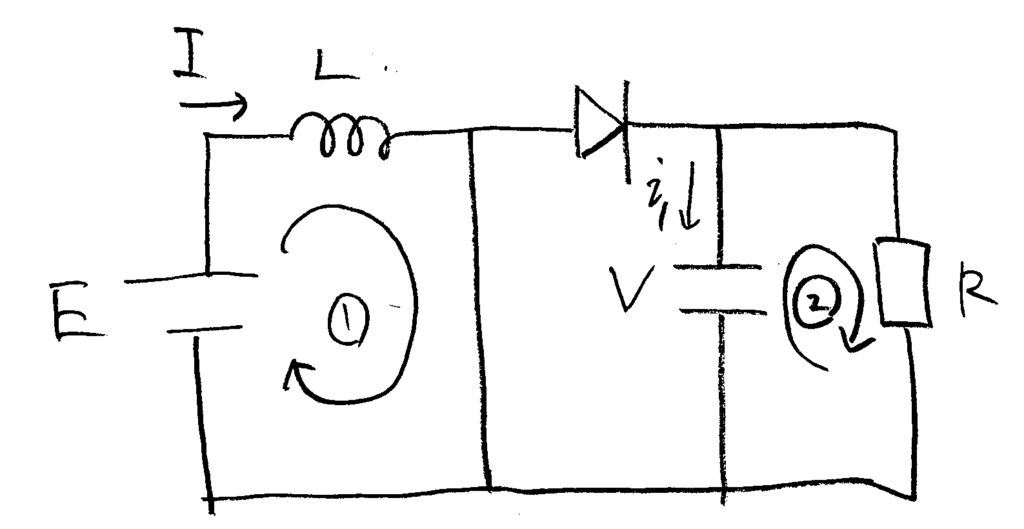
図のループ１でキルヒホッフ。$$E-L\frac{\Delta I_1}{\Delta t_1}=0$$ $$L\frac{\Delta I_1}{\Delta t_1}=E$$

図の方向に\(i_1\)を定義すると、$$\begin{align} i&=\frac{\Delta Q}{\Delta t_2}\\ &=\frac{C\Delta V_1}{\Delta t_2} \end{align}$$

図のループ2でキルヒホッフ。$$V-(-i)R=0$$ \(i\)を代入して整理して$$C\frac{\Delta V_1}{\Delta t_1}=-\frac{V}{R}$$

ル）ヲ）

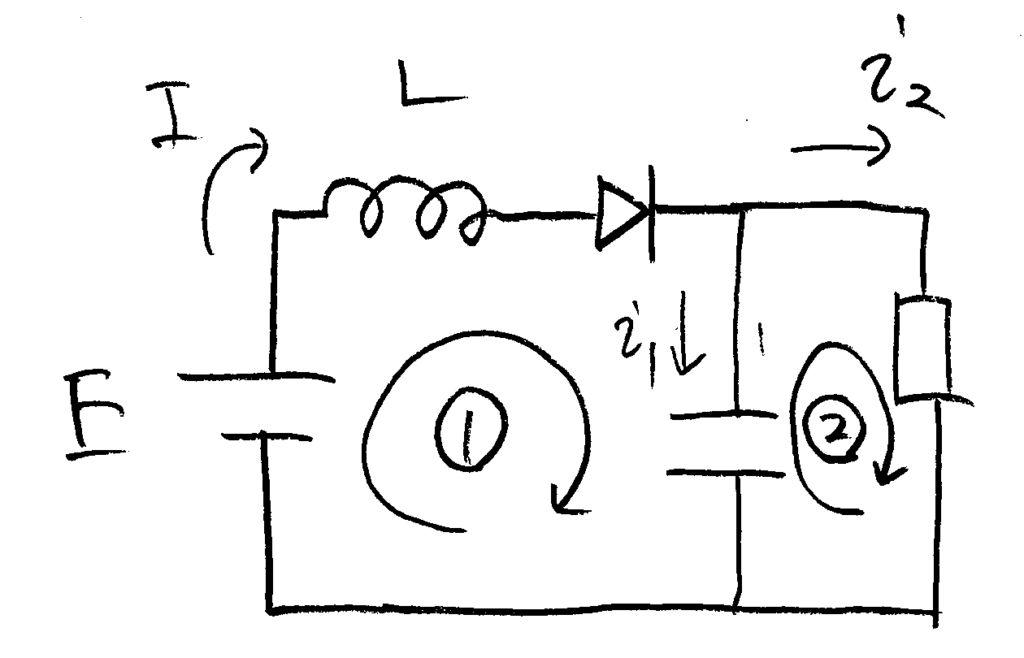
図のループ1でキルヒホッフ。$$E-L\frac{\Delta I_2}{\Delta t_2}-V=0$$ $$L\frac{\Delta I_2}{\Delta t_2}=E-V$$

図のように\(i_1, i_2\)を定義すると\(i_2=I-i_1\)。図のループ2でキルヒホッフ。$$V-i_2R=0$$ $$V=(I-i_1)R$$ $$\begin{align}\frac{V}{R}&=I-\frac{\Delta Q}{\Delta t_2}\\&=I-C\frac{\Delta V_2}{\Delta t_2}\end{align}$$ $$C\frac{\Delta V_2}{\Delta t_2}=I-\frac{V}{R}$$

問2

(iv)(v)式より$$\frac{\Delta I_1}{\Delta t_1}=\frac{E}{L}, \,\, \frac{\Delta I_2}{\Delta t_2}=\frac{E-V_0}{L}$$ \(\Delta I_1+\Delta I_2=0\)に代入して$$\frac{E}{L}\Delta t_1+\frac{E-V_0}{L}\Delta t_2=0$$ $$(\alpha E+E-V_0)\Delta t_2=0$$ $$V_0=E(1+\alpha)$$

また(iv)(v)式より$$\Delta V_1=-\frac{V}{CR}\Delta t_1, \,\, \Delta V_2=\frac{1}{C}\left(I_0-\frac{V}{R}\right)\Delta t_2$$ \(\Delta V_1+\Delta V_2=0\)に代入して$$-\frac{V}{CR}\alpha+\frac{1}{C}\left(I_0-\frac{V}{R}\right)=0$$ 解いて$$\begin{align}I_0&=\frac{1+\alpha}{R}V_0\\ &=\frac{E}{R}(1+\alpha)^2\end{align}$$

問3

図4において、\(V=V_0\)の一定値とみなすので、抵抗には常に電圧\(V_0\)がかかっている。抵抗での消費電力は$$\frac{V_0^2}{R}=(1+\alpha)^2\frac{E^2}{R}$$

図5は抵抗に電圧\(E\)がかかるので、電力は\(\frac{E^2}{R}\)

よって\((1+\alpha)^2\)倍

コメント

またしても問題文が長いのが第一印象。大問1に比べれば引っかかるポイントは少ない。丁寧に問題を読んで追いかけていけば試験中でも完答できそう。しかしじっくりやっていく時間がやっぱりネック。

回路の式(i)～(v)みたいなのはキルヒホッフを使うしかないわけだが、素早く出せるようにしっかりトレーニングが必要。