2020岡山大学 物理第4問 光波、複スリットの干渉
⑴
ア… \(\frac{1}{n}\) イ…1 ウ… \(n\)
屈折率は、振動数が不変で光速が\(\frac{1}{n}\) となるものだ、と覚えておきましょう。
⑵
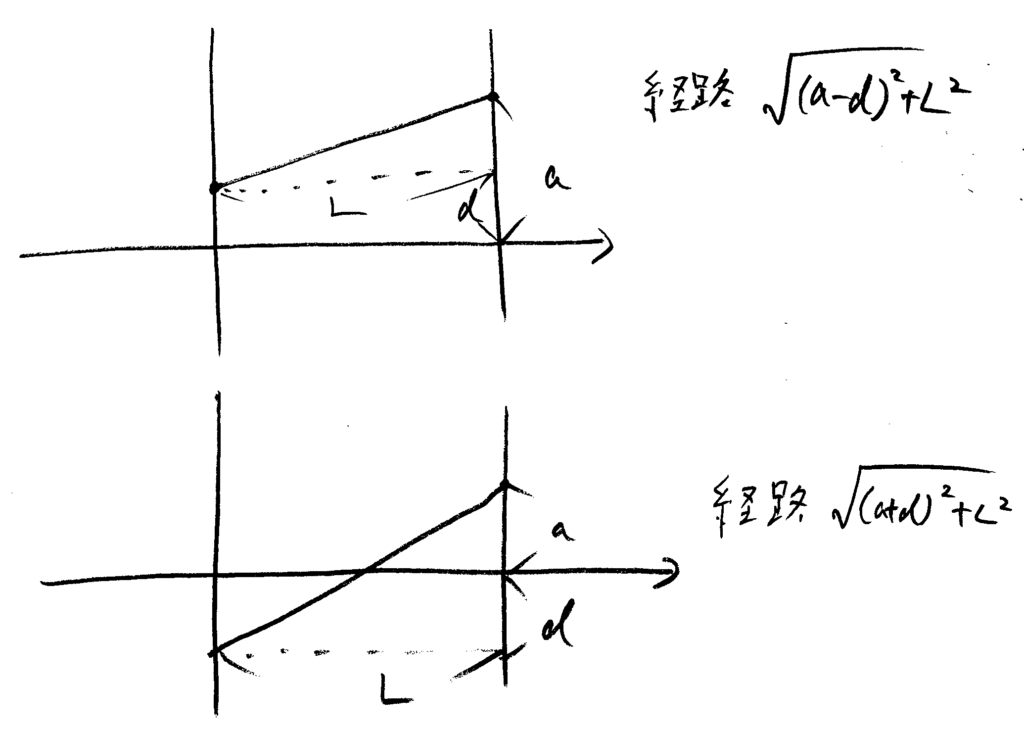
経路…幾何学的な距離。 光路…経路に屈折率をかけたもの。
$$n\sqrt{(a+d)^2+L^2}-n\sqrt{(a-d)^2+L^2}$$
⑶
\(x\)軸上では光路差は0。最も近い暗線は光路差が\(\pm\frac{\lambda}{2}\) 。光路差は$$\begin{align} n\sqrt{(b+d)^2+L^2}-n\sqrt{(b-d)^2+L^2}& \sim nL\left(1+\frac{(b+d)^2}{2L^2}\right)-nL\left(1+\frac{(b-d)^2}{2L^2}\right) \\&=nL\cdot\frac{4bd}{2L^2} \\&= \frac{2nbd}{L} \end{align}$$
よって$$\pm\frac{\lambda}{2}=\frac{2nbd}{L}$$ $$b=\pm\frac{\lambda L}{4nd}$$
⑷
複スリットよりも右の光路差は⑶と同じ。複スリットよりも左の光路差を考える。$$\begin{align} n\sqrt{(2d^2)+D^2}-nD&\sim nD\left(1+\frac{2d^2}{D^2}\right)-nD\\ &=\frac{2nd^2}{D} \end{align}$$ よって、暗線の\(y\)座標を\(b^\prime\)とすると、光路差は合計で$$\frac{2nd^2}{D}+\frac{2nb^\prime d}{L}=\pm\frac{\lambda}{2}$$ 解いて $$b^\prime=\pm\frac{\lambda L}{4nd}-\frac{Ld}{D}$$
暗線の位置は\(-\frac{Ld}{D}\)移動している。
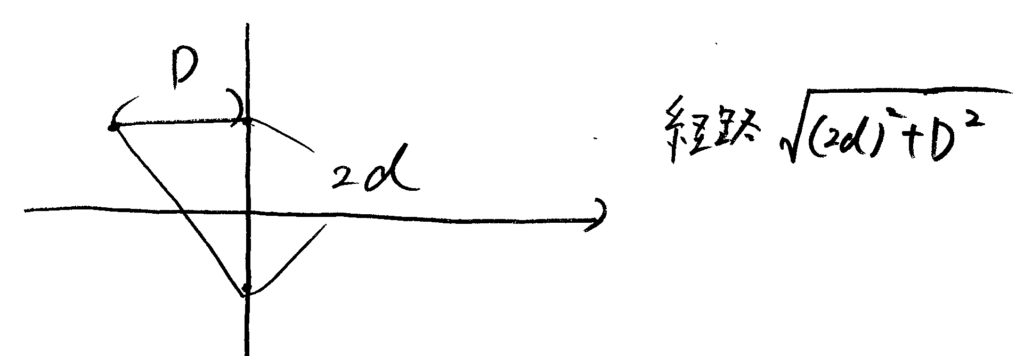
⑸
⑷の値に代入するだけ。\(-2.0\times10^{-4}\) m
[コメント] 基本的な光路差の問題。図形の問題だと思って経路を計算する。⑸の存在意義は…?